Fortunately, at that point I already know how to calculate the capacity of quantum channels, because I was involved in this endeavor during what is now known as the "heydays" of quantum information theory. I knew that in order to calculate the capacity for the black hole to transmit classical information, I had to calculate the shared entropy between a "preparer" and the radiation observed at future infinity. The preparer creates the physical quantum states that are to be used as signals (our particles and anti-particles) according to a list of symbols. So, if you want to send "0010011", then the preparer sends "ppappaa", where "p" stands for particle and "a" for anti-particle. The entropy of the preparer is just the entropy of the symbols she sends. Fairly quickly, I realize that the shared entropy has just the form that appears in Holevo's theorem. At that point, I see that it is all over, because the capacity of the black hole channel is just the Holevo capacity, as it should be. And it is also clear that if there is no stimulated emission, then the capacity is exactly zero and we have to look for someone or something to sue.
But now (back in 2004) we hear that Hawking is going to give a talk in Ireland where he will announce that he solved the black hole information paradox. He will announce (we hear), that he was wrong all along, that information is preserved in black holes. Greg and I are dumbfounded. Has he figured this out at the same time as we did? I start writing up our results like there is no tomorrow, but can't finish until a day after Hawking gives his talk. And we read the reports, and exhale. His "solution" has nothing to do with ours, and many physicists are very skeptical whether it is a solution at all.
At almost exactly this point, Charles Seife from Science Magazine calls me to comment on Hawking's "discovery", and I explain to him my thoughts, but can't hold back my excitement about what we found. That's the history of my comments in the article he wrote here.
So what happens now? Now comes a period where we submit our paper to Physical Review Letters, and fight with referees for two years.
But we also realize that what the black hole is doing by stimulating the emission of radiation is to act like a quantum cloning machine, and that we should calculate the cloning fidelity. This we do, and the results are incredible. First, we notice that the mathematics of cloning is exactly like that at work in stimulated emission in quantum optics, and that just as in the case of quantum optics, the fidelity of cloning is nearly optimal! Well, it is if the black hole can reflect a little bit of radiation. If it absorbs everything (and most people know that black holes don't necessarily absorb all radiation, it depends on the angular momentum of the incoming particle) then the fidelity of cloning is equal to the best you can do classically, namely classical state estimation. (In this case, classical state estimation comes down to Laplace's "rule of succession"). What this means is that if your initial quantum state has N particles in it, then you can reconstruct the initial state (using the particles that are emitted via stimulated emission, but without error correction!) with probability (N+1)/(N+2). This is also the estimated probability that the sun will rise tomorrow, given that you have observed it to rise N times in the past! Go figure.
Then we submit that paper to PRL And then things go from bad to worse. After another endless series of reviews (which admittedly are difficult because how many quantum gravity experts are also experts in quantum information theory and quantum cloning?) we finally give up, after receiving an (unsigned) Division Associate Editor (DAE) report that is, well how can I put it, angry? The report is 11 pages long, and I'm pretty sure who wrote it. But I'm determined to remain a gentleman.
I decide to lay low for a while, in particular because I have other papers to write. For about six years I lay low, give or take. But my interest is renewed when I see a paper by Kamil Bradler on the capacity of the Unruh channel. The Unruh channel, as you can imagine, is kind of like the "Hawking channel", where the noise is not Hawking radiation but rather Unruh radiation. You guessed it. And Bradler flat-out calculates this capacity while acknowledging that we had derived the same exact result for black holes earlier! (You can get his paper from arxiv here). And he also notices that these are all cloning channels!
So I decide to take my four-page article and turn it into a long article for Physical Review D, acknowledging that it is simply too much for PRL. Well, and then I register for the APS March meting to talk about the paper.
My talk at the meeting was, well, eventful: the device that switches one laptop to another to display slides froze my computer. I started to talk while the session chair tried to reboot my computer, log in while I'm talking, then the computer quits and shows black screen. I decide to give the talk entirely without slides, which is just as well: the point I was trying to make can be conveyed with flailing arms only.
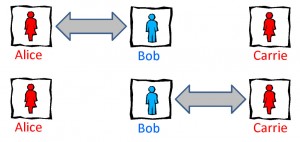
After the talk, I am asked whether stimulated emission by any chance sheds light on the AMPS controversy. This discussion, also known as the "firewall controversy", is about another paradox engendered by black holes. Without being too technical, the paradox involves the impossibility of being maximally entangled with two different systems (see John Preskill's description of the paradox).
Now, it turns out that when you read papers about the original suggestion by Almheiri, Marolf, Polchinsky, and Sully—hence "AMPS"— (and there has been a deluge of such papers since the AMPS paper first appeared), there is very little calculation going on. Shouldn't we try to calculate what the entanglement of Alice (who is thrown into a black hole) actually looks like? Well, if you neglect stimulated emission, you can't really do this calculation. In particular, nobody (from what I can tell), is trying to write down the joint wavefunction of the black hole, the stuff that formed it (or at least a piece of that stuff), as well as Alice being thrown into the mix at late times, and becoming entangled with it. But it turns out this is precisely what we have calculated in our paper here. If you skip to section 4 of that paper, that's where we discuss late-time particles accreting on the already formed black hole. I don't write down the joint wavefunction there but I have it in my notes, of course. There is no problem with entanglement monogamy, mainly because one of the central assumptions of AMPS, namely that the "Hawking radiation is pure", is incorrect. Hawking radiation is not pure at all. It is entangled with the black hole alright, but because of the presence of stimulated radiation, it is classically uncorrelated. This is not surprising because measuring Hawking radiation, after all, tells you nothing about the black hole. All the information is contained in the stimulated radiation.
I am reminded of the logical inference that if you start out with a statement that is false, you can derive any number of falsehoods from it. In the same manner, if you begin with a paradox (neglecting stimulated emission of radiation) you can generate an infinite number of other paradoxes from it.
I'm perfectly aware that I may be wrong. But let us first agree that:
1.) we should do calculations
2.) we should start with the right physics
Then let the chips fall where they may.
My talk at the meeting was, well, eventful: the device that switches one laptop to another to display slides froze my computer. I started to talk while the session chair tried to reboot my computer, log in while I'm talking, then the computer quits and shows black screen. I decide to give the talk entirely without slides, which is just as well: the point I was trying to make can be conveyed with flailing arms only.
After the talk, I am asked whether stimulated emission by any chance sheds light on the AMPS controversy. This discussion, also known as the "firewall controversy", is about another paradox engendered by black holes. Without being too technical, the paradox involves the impossibility of being maximally entangled with two different systems (see John Preskill's description of the paradox).
(Illustration: Courtesy of John Preskill)
Now, it turns out that when you read papers about the original suggestion by Almheiri, Marolf, Polchinsky, and Sully—hence "AMPS"— (and there has been a deluge of such papers since the AMPS paper first appeared), there is very little calculation going on. Shouldn't we try to calculate what the entanglement of Alice (who is thrown into a black hole) actually looks like? Well, if you neglect stimulated emission, you can't really do this calculation. In particular, nobody (from what I can tell), is trying to write down the joint wavefunction of the black hole, the stuff that formed it (or at least a piece of that stuff), as well as Alice being thrown into the mix at late times, and becoming entangled with it. But it turns out this is precisely what we have calculated in our paper here. If you skip to section 4 of that paper, that's where we discuss late-time particles accreting on the already formed black hole. I don't write down the joint wavefunction there but I have it in my notes, of course. There is no problem with entanglement monogamy, mainly because one of the central assumptions of AMPS, namely that the "Hawking radiation is pure", is incorrect. Hawking radiation is not pure at all. It is entangled with the black hole alright, but because of the presence of stimulated radiation, it is classically uncorrelated. This is not surprising because measuring Hawking radiation, after all, tells you nothing about the black hole. All the information is contained in the stimulated radiation.
I am reminded of the logical inference that if you start out with a statement that is false, you can derive any number of falsehoods from it. In the same manner, if you begin with a paradox (neglecting stimulated emission of radiation) you can generate an infinite number of other paradoxes from it.
I'm perfectly aware that I may be wrong. But let us first agree that:
1.) we should do calculations
2.) we should start with the right physics
Then let the chips fall where they may.