For this series of posts, I'm going to take you on a ride through the bewildering jungle that is quantum measurement. I've no idea how many parts will be enough, but I'm fairly sure there will be more than one. After all, the quantum mechanics of measurement has been that subject's "mystery of mysteries" for ages, it now seems.
Read MoreWhose entropy is it anyway? (Part 2: The so-called Second Law)
This is the second part of the "Whose entropy is it anyway?" series. Part 1: "Boltzmann, Shannon, and Gibbs" is here.
Yes, let's talk about that second law in light of the fact we just established, namely that Boltzmann and Shannon entropy are fundamentally describing the same thing: they are measures of uncertainty applied to different realms of inquiry, making us thankful that Johnny vN was smart enough to see this right away.
Whose entropy is it anyway? (Part 1: Boltzmann, Shannon, and Gibbs )
Note: this post was slated to appear on May 31, 2014, but events outside of my control (such as grant submission deadlines, and parties at my house) delayed its issuance.
The word "entropy" is used a lot, isn't it? OK, not in your average conversation, but it is a staple of conversations between some scientists, but certainly all nerds and geeks. You have read my introduction to information theory I suppose (and if not, go ahead and start here, right away!) But in my explanations of Shannon's entropy concept, I only obliquely referred to another "entropy": that which came before Shannon: the thermodynamic entropy concept of Boltzmann and Gibbs. The concept was originally discussed by Clausius, but because he did not give a formula, I will just have to ignore him here.
Why do these seemingly disparate concepts have the same name? How are they related? And what does this tell us about the second law of thermodynamics?
This is the blog post (possibly a series) where I try to throw some light on that relationship. I suspect that what follows below isn't very original (otherwise I probably should have written it up in a paper), but I have to admit that I didn't really check. I did write about some of these issues in an article that was published in a Festschrift on the occasion of the 85th birthday of Gerry Brown, who was my Ph.D. co-advisor and a strong influence on my scientific career. He passed away a year ago to this day, and I have not yet found a way to remember him properly. Perhaps a blog post on the relationship between thermodynamics and information theory is appropriate, as it bridges a subject Gerry taught often (Thermodynamics) with a subject I have come to love: the concept of information. But face it: a book chapter doesn't get a lot of readership. Fortunately, you can read it on arxiv here, and I urge you to because it does talk about Gerry in the introduction.
Gerry Brown (1926-2013)
Before we get to the relationship between Shannon's entropy and Boltzmann's, how did they end up being called by the same name? After all, one is a concept within the realm of physics, the other from electrical engineering. What gives?
The one to blame for this confluence is none other than John von Neumann, the mathematician, physicist, engineer, computer scientist (perhaps Artificial Life researcher, sometimes moonlighting as an economist). It is difficult to appreciate the genius that was John von Neumann, not the least because there aren't many people who are as broadly trained as he was. For me, the quote that fills me with awe comes from another genius who I've had the priviledge to know well, the physicist Hans Bethe. I should write a blog post about my recollections of our interactions, but there is already a write-up in the book memorializing Hans's life. While I have never asked Hans directly about his impressions of von Neumann (how I wish that I had!), he is quoted as saying (in the 1957 LIFE magazine article commemorating von Neumann's death: "I have sometimes wondered whether a brain like von Neumann's does not indicate a species superior to man".
The reason why I think that this quite a statement, is that I think Bethe's brain was in itself very unrepresentative of our species, and perhaps indicated an altogether different kind.
So, the story goes (as told by Myron Tribus in his 1971 article "Energy and Information")that when Claude Shannon had figured out his channel capacity theorem, he consulted von Neumann (both at Princeton at the time) about what he should call the "-p log p" value of the message to be sent over a channel. von Neumann supposedly replied:
"You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name. In the second place, and more importantly, no one knows what entropy really is, so in a debate you will always have the advantage.”
The quote is also reprinted in the fairly well-known book "Maxwell's Demon: Entropy, Information, and Computing", edited by Leff and Rex. Indeed, von Neumann had defined a quantity just like that as early as 1927 in the context of quantum mechanics (I'll get to that). So he knew exactly what he was talking about.
Let's assume that this is an authentic quote. I can see how it could be authentic, because the thermodynamic concept of entropy (due to the Austrian physicist Ludwig Boltzmann) can be quite, let's say, challenging. I'm perfectly happy to report that I did not understand it for the longest time, in fact not until I understood Shannon's entropy, and perhaps not until I understood quantum entropy.
Ludwig Boltzmann (1844-1906). Source: Wikimedia
Boltzmann defined entropy. In fact, his formula S=klogW is engraved on top of his tombstone, as shown here:
Google "Boltzmann tombstone" to see the entire marble edifice to Boltzmann
In this formula, S stands for entropy, k is now known as "Boltzmann's constant", and Wis the number of states (usually called "microstates" in statistical physics) a system can take on. But it is the logW that is the true entropy of the system. Entropy is actually a dimensionless quantity in thermodynamics. It takes on the form above (which has the dimensions of the constant k) if you fail to convert the energy units of temperature into more manageable units, such as the Kelvin. In fact, k just tells you how to do this translation:
where J (for Joule) is the SI unit for energy. If you define temperature in these units, then entropy is dimensionless
But this doesn't at all look like Shannon's formula, you say?
You're quite right. We still have a bit of work to do. We haven't yet exploited the fact that logW is the number of microstates consistent with a macrostate at energy E. Let us write down the probability distribution w(E) for the macrostate to be found with energy E. We can then see that
I'm sorry, that last derivation was censored. It would have bored the tears out of you. I know because I could barely stand it myself. I can tell you where to look it up in Landau & Lifshitz if you really want to see it.
The final result is this: Eq. (1) can be written as
implying that Boltzmann's entropy formula looks to be exactly the same as Shannon's.
Except, of course, that in the equation above the probabilities wi are all equal to each other. If some microstates are more likely than others, the entropy becomes simply
where the pi are the different probabilities to occupy the different microstate i.
Equation (3) was derived by the American theoretical physicist Willard Gibbs, who is generally credited for the development of statistical mechanics.
J. Willard Gibbs (1839-1903) Source: Wikimedia
Now Eq. (3) does precisely look like Shannon's, which you can check by comparing to Eq. (1) in the post "What is Information? (Part 3: Everything is conditional)". Thus, it is Gibbs's entropy that is like Shannon's, not Boltzmann's. But before I discuss this subtlety, ponder this:
At first sight, this similarity between Boltzmann's and Shannon's entropy appears ludicrous. Boltzmann was concerned with the dynamics of gases (and many-particle systems in general). Shannon wanted to understand whether you can communicate accurately over noisy channels. These appear to be completely unrelated endeavors. Except they are not, if you move far enough away from the particulars. Both, in the end, have to do with measurement.
If you want to communicate over a noisy channel, the difficult part is on the receiving end (even though you quickly find out that in order to be able to receive the message in its pristine form, you also have to do some work at the sender's end). Retrieving a message from a noisy channel requires that you or I make accurate measurements that can distinguish the signal from the noise.
If you want to characterize the state of a many-particle system, you have to do something other than measure the state of every particle (because that would be impossible). You'll have to develop a theory that allows us to quantify the state given a handful of proxy variables, such as energy, temperature, and pressure. This is, fundamentally, what thermodynamics is all about. But before you can think about what to measure in order to know the state of your system, you have to define what it is you don't know. This is Boltzmann's entropy: how much you don't know about the many-particle system.
In Shannon's channel, a message is simply a set of symbols that can encode meaning (they can refer to something). But before it has any meaning, it is just a vessel that can carry information. How much information? This is what's given by Shannon's entropy. Thus, the Shannon entropy quantifies how much information you could possibly send across the channel (per use of the channel), that is, entropy is potential information.
Of course, Boltzmann entropy is also potential information: If you knew the state of the many-particle system precisely, then the Boltzmann entropy would vanish. You (being an ardent student of thermodynamics) already know what is required to make a thermodynamical entropy vanish: the temperature of the system must be zero. This, incidentally, is the content of the third law of thermodynamics.
"The third law?", I hear some of you exclaim. "What about the second?"
Yes, what about this so-called Second Law?
To be continued, with special emphasis on the Second Law, in Part 2.
The science of citations. (Also: black holes, again).
If the title of this blog post made you click on it, I owe you an apology. All others, that is, those who got here via perfectly legitimate reasons, such as checking this blog with bated breath every morning--only to be disappointed yet again ... bear with me.
Here I'll tell you why I'm writing about the same idea (concerning, what else, the physics of black holes) for the fourth time.
You see, an eminent scientist (whose name I'm sure I forgot) once told me that if you want to get a new idea noticed among the gatekeepers of that particular field, you have to publish it five times. The same idea, he said, over and over.
I'm sure I listened when he said that, but I'm equally sure that, at the time (youthful as I was), I did not understand. Why would the idea, if it was new (and let's assume for the sake of the present argument) worthy of the attention and study of everyone working in the field, not take hold immediately?
Today I'm much wiser, because now I can understand this advice as being a perfectly commonplace application of the theory of fixation of beneficial alleles in Darwinian evolution.
Stop shaking your head already. I know you came here to get the latest on the physics of black holes. But before I get to that (and I will), this little detour on how science is made--via the mathematics of population genetics no less--should be worth your time.
In population genetics (the theory that deals with how populations and genes evolve), a mutation (that is, a genetic change) is said to have "gone to fixation" (or "fixated") if everybody in the population carries this mutation. This implies that all those that ever did NOT carry that mutation are extinct at the time of fixation. From the point of view of scientific innovation, fixation is the ultimate triumph of an idea: if you have achieved it, then nobody who ever did NOT believe you is dead as a doornail.
Fixation means you win. What do you have to do to achieve that?
Of course, in reality such "fixation of ideas" is never fully achieved, as in our world there will always be people who doubt that the Earth is round, or that the Earth revolves around the Sun, or that humans are complicit in the Earth's climate change. I will glibly ignore these elements. (As I'm sure you do too). Progress in science is hard enough even in the absence of such irrationality.
When a new idea is born, it is a fragile little thing. It germinates in the mind of its progenitor first tentatively, then more strongly. But even though it may one day be fully formed and forcefully expelled by its creative parent into the world of ideas, the nascent idea faces formidable challenges. It might be better than all other ideas in hindsight. But today is not hindsight: here, now, at the time of its birth, this idea is just an idea among many, and it can be snuffed out at a moment's notice.
The mathematics of population genetics teaches us that much: to calculate the probability of fixation of a mutation, you start by calculating its probability to go extinct. Let's think of a new idea as the mutation of an old idea.
What does it mean for an idea to go extinct? If we stick to ideas published in the standard technical literature, it means for that idea (neatly written into a publication) to never be cited because citations are, in a very real way, the offspring your idea germinates. You remember Mendel, the German-speaking Silesian monk who discerned the mathematical laws of inheritance at a time when Darwin was still entirely in the dark about how inheritance works?
Gregor Mendel (1822-1844) Source: Wikimedia
(Incidentally, my mother was born not far from Mendel's birthplace.)
Well, Mendel's idea almost got extinct. He published his work about the inheritance of traits in 1866, in the journal Verhandlungen des naturforschenden Vereins Brünn. Very likely, this is the most famous paper to ever appear in this journal, and to boot it carried the unfortunate title "Versuche über Pflanzenhybriden" (Experiments on Plant Hybridization). Choosing a bad title can really doom the future chances of your intellectual offspring (I know, I chose a number of such unfortunate titles), and so it was for Mendel. His paper was classified under "hybridization" (rather than "inheritance"), and lay dormant for 35 years. Imagine your work laying dormant for 35 years. Now stop.
The idea of Mendelian genetics was, for all purposes, extinct. But unlike life forms, extinct ideas can be resurrected. As luck would have it, a Dutch botanist by the name ofde Vries conducted a series of experiments hybridizing plant species in the 1890s, and came across Mendel's paper. While clearly influenced by that paper (because de Vries changed his nomenclature to match Mendel's), he did not cite him in his 1900 paper in the French journal Comptes Rendus de l'Académie des Sciences. And just like that, Mendel persisted in the state of extinction once more.
Except that this time, the German botanist and geneticist Carl Correns came to Mendel's rescue. Performing experiments on the hawkweed plant, he rediscovered Mendel's laws, and because he knew a botanist that had corresponded with Mendel, he was familiar with that work. Correns went on to chastize de Vries for not acknowledging Mendel, and after de Vries starting citing him, the lineage of Mendel's idea was established forever.
You may think that this is an extraordinary sequence of events but I can assure you, this is by no means an exception. Science does not progress in a linear predictable fashion, mostly because the agents involved (namely scientists) are not exactly predictable machines. They are people. Even in science, the fickle fortunes of chance reign supremely.
But chance can be described mathematically. Can we calculate the chance that a paper will become immortal?
Let us try to estimate the likelihood that a really cool paper (that advances science by a great deal) becomes so well-known that everybody in the field knows it (and therefore cites it, when appropriate). Let's assume that said paper is so good that it is better than other papers by a factor 1+s, where s is a positive fraction (s=0.1 if the paper is 10% better than the state of the art, for example). Even though this paper is "fitter"--so to speak--then all the other papers it competes with for attention, it is not obvious that it will become known instantly, because whether someone picks up the paper, reads it, understands it, and then writes a new paper citing it, is a stochastic (that is, probabilistic) process. So many things have to go right.
We can model these vagaries by using what is known as a Poisson process, and calculate the probability p(k) that a paper gets k citations
Poisson processes are very common in nature: any time you have rare events, the cumulative distribution (of how many of these rare events ended up occurring) is distributed like (1).
Note that because the mean number of citations of the paper (the average of the distribution), is 1+s and thus larger than one, and if we moreover assume that the papers that cite your masterpiece "inherit" the same advantage (because they also use that cool new idea) then in principle the number of citations of this paper should explode exponentially with time. But that is not a guarantee.
Let's calculate the probability P that the paper actually "takes off". In fact, it is easier to calculate the probability that it does NOT take off: that it languishes in obscurity forever. This is 1−P. (Being summarily ignored is the fate of several of my papers, and indeed almost all papers everywhere).
This (eternal obscurity) can happen if the paper never gets cited in the first place (given by p(0) in Eq. (1) above), plus the probability that it gets cited once (but the citing paper itself never gets cited: p(1)(1−P)) plus the probability that it gets cited twice, but BOTH citing papers don't make it: p(2)(1−P)2, and so on.
Of course, the terms with higher k become more and more unlikely (because when you get 10 citations, say, it is quite unlikely that all ten of them will never be cited). We can calculate the total "extinction probability" as an infinite sum:
but keep in mind that the sum is really dominated by its first few terms. Now we can plug formula (1) into (2), do a little dance, and you get the simple looking formula
That looks great, because you might think that we can now easily calculate P from s. But not so fast.
You see, that Eq. (3) is a recursive formula. It calculates P in terms of P. You are of course not surprised by that, because we explicitly assumed that the likelihood that the paper never becomes well known depends on the probability that the few papers that cite it are ignored too. Your idea becomes extinct if all those you ever influenced are reduced to silence, too.
While the formula cannot be solved analytically, you can calculate an approximate form by assuming that the paper is great but not world shaking. Then, the probability P that it will become well-known is small enough that we can approximate the exponential function in (3) as
that is, we keep terms up to quadratic in P. And the reason why P is small is because the advantage s isn't fantastically large either. So we'll ignore everything that has powers of s2 or higher in s.
Then Eq. (3) becomes
or
What we derived here is actually a celebrated result from population genetics, due to the mathematical biologist J. B. S. Haldane.
J. B. S. Haldane (1892-1964)
If you're not already familiar with this chap, spend a little time with him. (Like, reading about him on Wikipedia). He would have had a lot to complain about in this century, I'm thinking.
So what does this result teach us? If you take equation (4) and expand it to lowest order in s (this means, you neglect all terms of order s2), you get the result that is usually associated with Haldane, namely that the probability of fixation of an allele with fitness advantage s is
Here's what this means for us: if an idea is ten percent better than any other idea in the field, there is only a 20% chance that it will get accepted (via the chancy process of citation).
These are pretty poor odds for an obviously superior idea! What to make of that?
The solution to this conundrum is precisely the advice that the senior scientist imparted on me!
Try, try, again.
I will leave it to you, dear reader, to calculate the odds of achieving "fixation" if you start the process five independent times. (Bonus points for a formula that calculates the probability of fixation for n independent attempts at fixation).
So now we return to the first question. Why am I writing a fourth paper on the communication capacity of black holes (with a fifth firmly in preparation, I might mention)?
Because the odds that a single paper will spread a good idea are simply too small. Three is good. Four is better. Five is much better.
And in case you are trying to keep track, here is the litany of tries, with links when appropriate:
(1) C. Adami and G. ver Steeg. Class. Quantum Gravity 31 (2014) 075015 blogpost
(2) C. Adami and G. ver Steeg. quant-ph/0601065 (2006) [in review] blogpost
(3) K. Brádler and C. Adami, JHEP 1205 (2014) (also preprint arXiv:1310.7914) blogpost
(4) K. Brádler and C. Adami, arXiv preprint arXiv:1405.1097. Read below.
The last paper, entitled "Black holes as bosonic Gaussian channels" was written with my colleague Kamil Bradler (just as the paper that was the object of my most watched blog post to-date). In there we show, again, what happens to quantum information interacting with a black hole, only that in paper (3) we could make definitive statements only about two very extreme black hole channels: those that perfectly reflect information, and those that perfectly absorb. While we cannot calculate all capacities in the latest paper (4), we can do this now as accurately as current theory allows, using the physics of "Gaussian states", rather than the "qubits" that we used previously. Gaussian states are quantum superpositions of particles that are such that if you would measure them, you get a distribution (of the number of measured particles) that is Gaussian. Think of them was wavepackets, if you wish. They are very convenient in quantum optics, for example. And they turn out to be very convenient to describe black hole channels too.
So we are getting the message out one more time. And the message is loud and clear: Black holes don't mess with information. The Universe is fine.
Darwin inside the machine: A brief history of digital life
In 1863, the British writer Samuel Butler wrote a letter to the newspaper The Press entitled "Darwin Among the Machines". In this letter, Butler argued that machines had some sort of "mechanical life", and that machines would some day evolve to be more complex than people, and ultimately bring humanity into extinction:
"Day by day, however, the machines are gaining ground upon us; day by day we are becoming more subservient to them; more men are daily bound down as slaves to tend them, more men are daily devoting the energies of their whole lives to the development of mechanical life. The upshot is simply a question of time, but that the time will come when the machines will hold the real supremacy over the world and its inhabitants is what no person of a truly philosophic mind can for a moment question."
(S. Butler, 1863)
While futurist and doomsday prognosticator Ray Kurzweil would probably agree, I think that the realm of the machines is still far in the future. Here I would like to argue that Darwin isn't among the machines just yet, but he is certainly inside the machines.
The realization that you could observe life inside a computer was fairly big news in the early 1990s. The history of digital life has been chronicled before, but perhaps it is time for an update, because a lot has happened in twenty years. I will try to be brief: A Brief History of Digital Life. But you know how I have a tendency to fail in this department.
Who came up with the idea that life could be abstracted to such a degree that it could be implemented (mind you, this is not the same thing as simulated) inside a computer?
Why, that would be just the same guy who actually invented the computer architecture we all use! You all know who this is, but here's a pic anyway:
I don't have many scientific heroes, but he is perhaps my number one. He was first and foremost a mathematician (who also made fundamental contributions to theoretical physics). After he invented the von Neumann architecture of modern computers, he asked himself: could I create life in it?
Who would ask himself such a question? Well, Johnny did! He asked: if I could program an entity that contained the code that would create a copy of itself, would I have created life? Then he proceeded to try to program just such an entity, in terms of a cellular automaton (CA) that would self-replicate. Maybe you thought that Stephen Wolfram invented CAs? He might want to convince you of that, but the root of CAs goes back to Stanislaw Ulam, and indeed our hero Johnny. (If Johnny isn't your hero yet, I'll try to convince you that he should be. Did you know he invented Game Theory?) Johnny actually wrote a book called "Theory of Self-Reproducing Automata" that was only published after von Neumann's death. He died comparatively young, at age 54. Johnny was deeply involved in the Los Alamos effort to build an atomic bomb, and was present at the 1946 Bikini nuclear tests. He may have paid the ultimate prize for his service, dying of cancer likely due to radiation exposure. Incidentally Richard Feynman also succumbed to cancer from radiation, but he enjoyed a much longer life. We can only imagine what von Neumann could have given us had he had the privilege of living into his 90s, as for example Hans Bethe did. And just like that, I listed two other scientists on my hero list! They both are in my top 5.
All right, let's get back to terra firma. Johnny invented Cellular Automata just so that he can study self-replicating machines. What he did was create the universal constructor, albeit completely in theory. But he designed it in all detail: a 29-state cellular automaton that would (when executed) literally construct itself. It was a brave (and intricately detailed) construction, but he never got to implement it on an actual computer. This was done almost fifty years later by Nobili and Pesavento, who used a 32-state CA. They were able to show that von Neumann's construction ultimately was able to self-reproduce, and even led to the inheritance of mutations.
von Neumann used information coded in binary in a "tape" of cells to encode the actions of the automaton, which is quite remarkable given that DNA had yet to be discovered.
Perhaps because of von Neumann's untimely death, or perhaps because computers would soon be used for more "serious" applications than making self-replicating patterns, this work was not continued. It was only in the late 1980s that Artificial Life (in this case, creating a form of life inside of a computer) became fashionable again, when Chris Langton started the Artificial Life conferences in Santa Fe, New Mexico. While Langton's work focused also on implementations using CA, Steen Rasmussen at Los Alamos National Laboratory tried another approach: take the idea of computer viruses as a form of life seriously, and create life by giving self-replicating computer programs the ability to mutate. To do this, he created self-replicating computer programs out of a computer language that was known to support self-replication: "Redcode", the language used in the computer game Core War. In this game that was popular in the late 80s, the object is to force the opposing player's programs to terminate. One way to do this is to write a program that self-replicates.
Rasmussen created a simulated computer within a standard desktop, provided the self-replicator with a mutation instruction, and let it loose. What he saw was first of all quick proliferation of the self-replicator, followed by mutated programs that not only replicated inaccurately, but also wrote over the code of un-mutated copies. Soon enough no self-replicator with perfect fidelity would survive, and the entire population died out, inevitably. The experiment was in itself a failure, but it ultimately led to the emergence of digital life as we know it, because when Rasmussen demonstrated his "VENUS" simulator at the Santa Fe Institute, a young tropical ecologist was watching over his shoulder: Tom Ray of the University of Oklahoma. Tom quickly understood what he had to do in order to make the programs survive. First, he needed to give each program a write-protected space. Then, in order to make the programs evolvable, he needed to modify the programming language so that instructions did not refer directly to addresses in memory, simply because such a language turns out to be very fragile under mutations.
Ray went ahead and wrote his own simulator to implement these ideas, and called it tierra. Within the simulated world that Ray had created inside the computer, real information self-replicated, and mutated. I am writing "real" because clearly, the self-replicating programs are not simulated. They exist in the same manner as any computer program exists within a computer's memory: as instructions encoded in bits that themselves have a physical basis: different charge states of a capacitor.
The evolutionary dynamics that Ray observed was quite intricate. First, the 80 instruction-long self-replicator that Ray had painstakingly written himself started to evolve towards smaller sizes, shrinking, so to speak. And while Ray suspected that no program could self-replicate that was smaller than, say, 40 instructions long, he witnessed the sudden emergence of an organism that was only 20 lines long. These programs turned out to be parasites that "stole" the replication program of a "host" (while the programs were write-protected, Ray did not think he should insist on execution protection). Because the parasites did not need the "replication gene" they could be much smaller, and because the time it takes to make a copy is linear in the length of the program, these parasites replicated like crazy, and would threaten to drive the host programs to extinction.
But of course that wouldn't work, because the parasites relied on those hosts! Even better, before the parasites could wipe out the hosts, a new host emerged that could not be exploited by the parasite: the evolution of resistance. In fact, a very classic evolutionary arms race ensued, leading ultimately to a mutualistic society.
While what Ray observed was incontrovertibly evolution, the outcome of most experiments ended up being much of the same: shrinking program, evolution of parasites, an arms race, and ultimately coexistence. When I read that seminal 1992 paper [1] on a plane from Los Angeles to New York shortly after moving to the California Institute of Technology, I immediately started thinking about what one would need to do in order to make the programs do something useful. The tierran critters were getting energy for free, so they simply tried to replicate as fast as possible. But energy isn't free: programs should be doing work to gain that energy. And inside a computer, work is a calculation.
After my postdoctoral advisor Steve Koonin (a nuclear physicist, because the lab I moved to at Caltech was a nuclear theory lab) asked me (with a smirk) if I had liked any of the papers he had given me to read on the plane, I did not point to any of the light-cone QCD papers, I told him I liked that evolutionary one. He then asked: "Do you want to work on it?", and that was that.
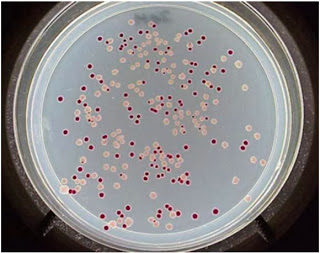
I started to rewrite tierra so that programs had to do math in order to get energy. The result was this paper, but I wasn't quite happy with tierra. I wanted it to do much more: I wanted the digital critters to grow in a true 2D space (like, say, on a Petri dish)
and I wanted them to evolve a complex metabolism based on computations. But writing computer code in C wasn't my forte: I was an old-school Fortran programmer. So I figured I'd pawn the task off to some summer undergraduate students. Two were visiting Caltech that summer: C. Titus Brown who was an undergrad in Mathematics at Reed College, and Charles Ofria, a computer science undergrad at Stony Brook University, where I had gotten my Ph.D. a few years earlier. I knew both of them because Titus is the son of theoretical physicist Gerry Brown, in whose lab I obtained my Ph.D, and Charles used to go to high schoolwith Titus.
Above is a photo taken during the summer when the first version of Avida was written, and if you clicked on any of the links above then you know that Titus and Charles have moved on from being undergrads. In fact, as fate would have it we are all back together here at Michigan State University, as the photo below documents. Where we were attempting to recreate that old polaroid!
The version of the Avida program that ultimately led to 20 years of research in digital evolution (and utlimately became one of the cornerstones of the BEACON Center) was the one written by Charles. (Whenever I asked any of the two to just modify Tom Ray's tierra, they invariably proceeded by rewriting everything from scratch. I clearly had a lot to learn about programming.)
So what became of this digital revolution of digital evolution? Besides germinating the BEACON Center for the Study of Evolution in Action, Avida has been used for more and more sophisticated experiments in evolution, and we think that we aren't done by a long shot. Avida is also used to teach evolution, in high-school and college class rooms.
Whenever I give a talk or class on the history of digital life (or even its future), I seem to invariably get one question that wonders whether revealing the power that is immanent in evolving computer viruses is, to some extent, reckless.
You see, while the path to the digital critters that we call "avidians" was never really inspired by real computer viruses, you had to be daft not to notice the parallel.
What if real computer viruses could mutate and adapt to their environment, almost instantly negating any and all design efforts of the anti-malware industry? Was this a real possibility?
Whenever I was asked this question, in a public talk or privately, I would equivocate. I would waffle. I had no idea. After a while I told myself: "Shouldn't we know the answer to this question? Is it possible to create a new class of computer viruses that would make all existing cyber-security efforts obsolete?"
Because if you think about it, computer viruses (the kind that infect your computer once in a while if you're not careful) already displays some signs of life. I'll show you here that one of the earliest computer viruses (known as the "Stoned" family) displayed one sign, namely the tell-tale waxing and waning of infection rate as a function of time.
Why does the infection rate rise and fall? Well, because the designers of the operating system (the Stoned virus infected other computers only by direct contact: an infected floppy disk) were furiously working on thwarting this threat. But the virus designers (well, nobody called them that, really--they were called "hackers") were just as furiously working on defeating any and all countermeasures. A real co-evolutionary arms race ensued, and the result was that the different types of Stoned viruses created in response to the selective pressure imparted by operating system designers could be rendered in terms of a phylogeny of viruses that is very reminiscent of the phylogeny of actual biochemical viruses (think influenza, see below).
What if these viruse could mutate autonomously (like real biochemical viruses) rather than wait for the "intelligent design" of hackers? Is this possible?
I did not know the answer to this question, but in 2006 I decided to find out.
And to find out, I had to try as hard as I could to achieve the dreaded outcome. The thinking was: If my lab, trained in all ways to make things evolve, cannot succeed in creating the next-generation malware threat, then perhaps no-one can. Yes, I realize that this is nowhere near a proof. But we had to start somewhere. But if we were able to do this, then we would know the vulnerabilities of our current cyber-infrastructure long before the hackers did. We would be playing white hat vs. black hat, for real. But we would do this completely secretly.
In order to do this, I talked to a private foundation, which agreed to provide funds for my lab to investigate the question, provided we kept strict security protocols. No work is to be carried out on computers connected to the Internet. All notebooks are to be kept locked up in a safe. Virus code is only transferred from computer to computer via CD-ROM, also to be stored in a safe. There were several other protocol guidelines, which I will spare you. The day after I received notice that I was awarded the grant, I went and purchased a safe.
To cut a too long story into a caricature of "short": it turned out to be exceedingly difficult to create evolving computer viruses. I could devote an entire blog post to outline all the failed approached that we took (and I suspect that such a post would be useful for some segments of my readership). My graduate student Dimitris Iliopoulos set up a computer (disconnected, of course) with a split brain: one where the virus evolution would take place, and one that monitored the population of viruses that replicated--not in a simulated environment--but rather in the brutal reality of a real computer's operating system.
Dimitris discovered that the viruses did not evolve to be more virulent. They became as tame as possible. Because we had a "watcher" program monitoring the virus population, (culling individuals in order to keep the population size constant) programs evolved to escape the atttention of this program. Because being noticed by said program would spell death, ultimately.
This strategy of "hiding" turns out to be fairly well-known amongst biochemial viruses, of course. But our work was not all in vane. We contacted one of the leading experts in computer security at the time, Hungarian-born Péter Ször, who worked at the computer security company Symantec and wrote the book on computer viruses. He literally wrote it: you can buy it on Amazon here.
When we first discussed the idea with Péter, he was skeptical. But he soon warmed up to the idea, and provided us with countless examples of how computer viruses adapt--sometimes by accident, sometimes by design. We ended up writing a paper together on the subject, which was all the rage at the Virus Bulletin conference in Ottawa, in 2008 [3]. You can read our paper by clicking on this link here.
Which bring me, finally, to the primary reason why I am reminiscing about the history of digital life, and my collaboration with Péter Ször in particular. Péter passed away suddenly just a few days ago. He was 43 years old. He worked at Symantec for the majority of his career, but later switched to McAfee Labs as Senior Director of Malware Research. Péter kept your PC (if you choose to use such a machine) relatively free from this artfully engineered brand of viruses for decades. He worried whether evolution could ultimately outsmart his defenses and, at least for this brief moment in time, we thought we could.
[1] T.S. Ray, An approach to the synthesis of life, In: Langton, C., C. Taylor, J. D. Farmer, & S. Rasmussen [eds], Artificial Life II, Santa Fe Institute Studies in the Sciences of Complexity, vol. XI, 371-408. Redwood City, CA: Addison-Wesley.
[2] S. White, J. Kephart, D. Chess. Computer Viruses: A Global Perspective. In: Proceedings of the 5th Virus Bulletin International Conference, Boston, September 20-22, 1995, Virus Bulletin Ltd, Abingdon, England, pp. 165-181. September 1995
[3] D. Iliopoulos, C. Adami, and P. Ször. Darwin Inside the Machines: Malware Evolution and the Consequences for Computer Security (2009). In: Proceedings of VB2008 (Ottawa), H. Martin ed., pp. 187-194













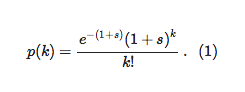



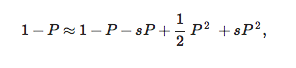










![Incidents of infection with the "Stoned" virus over time, courtesy of [2].](https://images.squarespace-cdn.com/content/v1/53308268e4b00147ec53e8b4/1395928284364-1PXH8XG3GQAZQ2XQQNIH/image-asset.png)


