According to the "MIT Technology Review", the world of game theory is "currently on fire". To be sure, I am not the arsonist. But, judging by the interest a paper by Bill Press and Freeman Dyson that was published a year ago in the Proceedings of the National Academy of Sciences has created, the flamboyant description is not completely off the mark. Before I describe the contents of the Press and Dyson paper (which has been done, to be sure, by many a blogger before me, see here or here), let me briefly tell you about the authors.
I know both of them in different ways. Bill Press is a Professor of Computer Science as well as Professor of Integrative Biology at UT Austin. Incidentally, UT Austin is a sister campus within the BEACON Center for the Study of Evolution in Action, which I also belong to here at Michigan State University. Bill Press is an astrophysicist by training, but perhaps most famous for a book on scientific computing, called "Numerical Recipes". That's where I know him from. If you've used scientific computing in the 90s and 00s, say, then you know this book. Bill Press is also the President of the American Association for the Advancement of Science (AAAS), which you may know as the publisher of Science Magazine. AAAS elected me a fellow in 2011, so I'm perfectly happy with this organization, as you can imagine. Press was also a "Prize Postdoctoral Fellow" at Caltech (incidentally as was I), and actually grew up in Pasadena (I spent almost 20 years there). So, besides the fact that he is way more famous than I am, there are some interesting parallels in our careers. I was once offered a Director's postdoc fellowship at Los Alamos National Laboratory that I declined. He accepted the Deputy Laboratory Director position there in 1998. He worked on black hole physics and is kinda famous for his work with Teukolsky. I worked on black hole physics… and if you read this blog then you know that story. So the parallels are, at best, marginal. He now works in computational biology, and I work there too, and that's where this story really has its beginning.
I've known of Freeman Dyson ever since I took Quantum Field Theory in grad school at SUNY Stony Brook. I can't and won't sing his praises here because my blog posts tend to be on the long side to begin with. I will probably always be able to write down the Schwinger-Dyson equation, perhaps even when somewhat inebriated (but I've never tried this). I've met him a couple of times but I do not expect that he would remember me. He is 89 now, so many people were surprised to hear that the mathematics of the PNAS paper mentioned above were entirely his (as recounted here). I'm not that surprised, because I've known the theoretical physicist Hans Bethe quite well in the last thirteen years of his life, and he was still able to calculate. And Bethe was 85 when I first met him. So I know that this is possible as long as you do not stop.
So, what did Press and Dyson do? To begin to understand this, you have to have heard of the "Prisoner's Dilemma".
The Prisoner's Dilemma (PD for short), is a simple game. Two players, two moves. The back story is a bit contrived: Two shady characters commit a crime, but are discovered as they flee the scene, speedily.
The authorities nab both of them, but are unsure which of the two is the actual perpetrator. They are ready to slap a "speeding while leaving a crime scene" conviction on both of them ("What, no grand-jury indictment? Have you even heard of "trial by jury of peers"?), when they are interrogated one more time, separately.
"Listen", the grand interrogator whispers to one of them, "you can go scot-free if you tell me it was the other guy". "Whoa. An incentive.", thinks perp. No. 1. "I get one year for accelerated haste, but I get 5 years if they figure we both were in on the heist". "If I say nothing we both get a year, and are out by Christmas on good behavior. But if they offer the same deal to my buddy, I bet he squeals like a pig. He gets out, and I go in for 20. I better rat him out". As a consequence, they rat each other out and spend 5 years in the slammer. They could have both spent Christmas at home. But instead, they chose to "defect" rather than "cooperate". How lame!
Theory says, actually, not lame at all. Theory says: "Under these circumstances, thou shalt betray your fellow man!" That theory, by the way, is due to no other than John Forbes Nash
, who even got a Nobel for it. Well, John von Neumann, the all-around genius and originator of Game Theory would have had a few choice words for that prize, but that's for another blog. "A Nobel for applying Brouwer's fixed point theorem? Are you f***ing kidding me?", is what Johnny might have said. (von Neumann's friends called him Johnny. I doubt anybody called Nash 'Johnny'). But let's agree not to digress.
So, Nash says: "Screwing your adversary is the rational choice in this situation". And that's certainly correct. The aforementioned fixed point theorem guarantees it. Nowadays, you can derive the result in a single line. And you thought Nobel prizes are hard to get? Well, today you may have to work a bit harder than that.
Here then, is the dilemma in a nut shell. "If we both cooperate by not ratting each other out, we go home by Christmas". But there is this temptation: "I rat out the other guy and I go free, like, now (and the other guy won't smell flowers until the fourth Clinton administration). But if we both rat each other out, then we may regret that for a long time."
You can view the dilemma in terms of a payoff matrix as follows. A matrix? Don't worry: it's just a way to arrange numbers. We both keep silent: one year for each of us. We both rat each other out: 3 years for each of us, because now the cops are certain we did it. But if I rat you out while you're being saintly…. then I go free and you spend serious time (like, 20 years). Of course, the converse holds true too: If I hold my breath while you squeal, then and I am caught holding the bag.
We can translate the "time-in-the-slammer" into a payoff-to-the-individual instead like this: hard time=low payoff. Scot-free=high payoff. You get the drift. We can then write a payoff matrix for the four possible plays. Staying silent is a form of cooperation, so we say this move is "C". Ratting out is a form of defection, so we call this move "D'.
The four possible plays are now: we both cooperate: "CC" (payoff=3), we both defect: "DD" (payoff=1), and we play unequally: "CD" or "DC". If I cooperate while you defect, I get nada and you get 5. Of course, the converse is true if I defect and you cooperate. So let's arrange that into a matrix:
The matrix entry contains the payoff to the "row player", that is, the player on "the left of the matrix", as opposed to the top. Two players could do well by cooperating (and earning 3s), while the rational choice is both players defect, earning 1s each. What gives?
What gives is, the perps are not allowed to talk to each other! If they could, they'd certainly conspire to not rat each other out. I've made this point in a paper three years ago that was summarily ignored by the community. (I concede that, perhaps, I didn't choose a very catchy title.) Still, I'm bitter. Moving on.
How could players, engaged in this dilemma, communicate? Communication in this case entails that players recognize each other. "Are you one of these cheaters, or else a bleeding-heart do-gooder?" is what every player may want to know before engaging the adversary. How could you find out? Well, for example, by observing your opponent's past moves! This will quickly tell you what kind of an animal you're dealing with. So a communicator's strategy should be to make her moves conditional on the opponent's past moves (while not forgetting what you yourself did last time you played).
So let's imagine I (and my opponent) make our moves conditional on what we just did the last time we played. Because there are four possible histories (CC, CD, DC, and DD, meaning, the last time we played, I played C and you played C, or I played C and you played D, etc.) Now instead of a strategy such as "I play C no matter what you do!" I could have a more nuanced response, such as: "If I played C (believing in the good of mankind) and you played D (ripping me off, darn you) then I will play D, thank you very much!". Such nuanced strategies are clearly far more effective than unconditional strategies, because they are responsive to the context of the opponent's play, given your own.
Strategies that make their choice dependent on previous choices are communicating. Such communicating strategies are a relatively new addition to the canon of evolutionary game theory (even though one of the "standard" strategies called "Tit-for-Tat", is actually a strategy that communicates). Because this strategy ("TFT" for short) will come up later, let me quickly introduce you to it: TFT does to its opponent what the opponent just did to TFT
So, TFT is sort of an automaton replaying the Golden Rule, isn't it? "I'll do unto you what you just did to me!" Indeed, it kinda is, and and it is quite a successful strategy all in all. Let me introduce a notation to keep track of strategies, here. It will look like math, but you really should think of it as a way to keep track of stuff.
So, I can either cooperate or defect. That means, I either play option "C" or option "D". But you know, I reserve the right to simply have a bias for one or the other choice. So my strategy should really be a probability to play C or D. Call this probability $p$. Keep in mind that this probability is the probability to cooperate. The probability to defect will be $1-p$.
If communication is involved, this probability should be dependent on what I just learned (my opponent's last play). The last exchange is four possible situations: CC, CD, DC, an DD: the first: I and my opponent just played "C", the last one: I and my opponent just played "D". A strategy then is a set of four probabilities $$ p(CC), p(CD), p(DC), p(DD). $$ Here, $p(CC)$ is the probability to cooperate if my previous move was 'C' and my opponent's was 'C' also, and so on. Clearly, armed with such a set of probabilities, you can adjust your probability to cooperate to what your opponent plays. The TFT strategy, by the way, would be given in terms of this nomenclature as TFT=(1,0,1,0), that is, TFT cooperates if the opponent's last move was "C", and defects otherwise. What other strategies are out there, if the probabilities can be arbitrary, not just zero and one?
That's the question Bill Press asked himself. Being a computational guy, he figured he'd write a program that would have all possible strategies play against all other possible strategies. Good idea, until the supercomputers he enlisted for this task started to crash. The reason why Press's computers were crashing (according to him, in an interview at Edge.org), was that he assumed that the payoff that a strategy would receive would depend on the way it played (that is, the four probabilities written above).
Well, you would think that, wouldn't you? I certainly would have. Me and my opponent both have four probabilities that define the way we play. I would assume that my average payoff (assuming that we play against each other a really long time), as well as my opponent's average payoff, will depend on these eight probabilities.
That is where you would be wrong, and Freeman Dyson (according to Press) sent Press a proof that this was wrong the next day. The proof is actually fairly elegant. What Dyson proved is that one player (let us call her "ZD") can choose her four probabilities judiciously in such a manner that the opponent will receive a payoff that only depends on ZD's strategy, and nothing else.
ZD, by the way, does not stand for Zooey Deschanel, but rather "Zero Determinant", which is a key trick in Dyson's proof. I thought I might clarify that.
The opponent (let's call him "O") can do whatever he wants. He can change strategy. He can wail. He can appeal to a higher authority. He can start a petition on Change.org. It won't make a dime of a difference. ZD can change her strategy (while still staying within the realm of judiciously chosen "ZD strategies", and change O's payoff. Unilaterally. Manipulatively. Deviously.
To do this, all that ZD has to do ist to set two of her probabilities to be a very specific function of the two others. I can show you exactly how to do this, but the formula is unlikely to enlighten you.
OK, fine, you can see it, but I'll just give you the simplified version that uses the payoffs in the matrix I wrote above (you know, the one with 5,3,1, and 0 in it), rather than the general case described by Press and Dyson. Let's also rename the clunkish $$p(CC), p(CD), p(DC), p(DD)$$ as $$p_1,p_2,p_3,p_4$$
Then, all ZD has to do is to choose $$p_2=2p_1-1+p_4$$ $$p_3=\frac12(1-p_1+3p_4)$$
See, I told you that this isn't particularly enlightening. But you can see that there is a whole set of these strategies, defined by a pair of probabilities $p_1,p_4$. These can be arbitrary within bounds: they have to be chosen such that $p_2$ and $p_3$ are between zero and one.
So let's take a step back. ZD can be mean and force O to accept a payoff he does not care for, and cannot change. Does ZD now hold the One Ring that makes the Golden Rule a quaint reminder of an antiquated and childish belief in the greater good?
Not so fast. First, ZD's payoff under the strategy she plays isn't exactly the cat's meow. For example, if ZD's opponent plays "All-D" (that is, the strategy (0,0,0,0) that is the game-theoretic equivalent of the current Republican-dominated congress: "No,no.no,no") ZD forces All-D to take a constant payoff alright, but this is higher than what ZD receives herself! This is because ZD's payoffs do depend on all eight probabilities (well, six, because two have been fixed by playing a ZD strategy), and playing All-D does not make you rich, if you play ZD or not. So you better not play ZD against All-D, but you might be lucky against some others.
Take, for example, one of the best communicating strategies ever designed, one called either "Win-Stay-Lose-Shift" (WSLS), or alternatively "Pavlov". WSLS was invented by Martin Nowak and Karl Sigmund in a fairly famous Nature paper. This strategy is simple: continue doing what you're doing when you're winning, but change what you do when you lose. So, for example, if you and your opponent cooperate, then you should be cooperating next time ('cause getting a '3' is winning). Hence, $p_1=1$. On the contrary, if you just played 'D' and so did your opponent, this would not be called winning, so you should switch from defection to cooperation. Thus, $p_4=1$. If you played 'C' and your opponent suckered you with a 'D', then that is definitely not called winning, so you should switch to 'D' next: $p_2=0$. If you instead played 'D' to the hapless opponent's 'C', well that's a major win, and you should continue what you're doing: $p_3=0$.
How does WSLS fare against ZD? Well, WSLS gets handed his lunch! ZD sweeps the floor with WSLS. I can give you the mean expected payoff that WSLS gets when playing a perfectly vanilla ZD with $p_1=0.99$ and $p_4=0.01$. (That's a ZD strategy that likes to cooperate, but is fairly unforgiving.) WSLS get an average of 2 against this strategy, just as much as any other strategy will gain. If ZD is playing those numbers, it doesn't matter what you do. You get two and like it. That's the whole point. ZD is a bully.
What does ZD get against WSLS? What ZD receives generally (against any opposing strategy) is a more complicated calculation. It's not terribly hard but it requires pencil and paper. A lot of pencil and paper, to be exact. (OK, fine, maybe not for everyone, required a lot of pencil and paper. And eraser. A lot of eraser.) The result is too large to show on this blog, so: sorry!
Alright, this is not the days of Fermat because we can link stuff, so there it is, linked. You learned nothing from that. If you plug in the WSLS strategy (1,0,0,1) into that unwieldy formula you just not looked at, you get:
The mean payoff a ZD strategy defined by $p_1=0.99, p_4=0.01$ receives from WSLS is $11/27\approx 2.455$. That's a lot more than what WSLS gets (namely 2). That's Grand Larceny, isn't it? ZD the victorious bully, while WSLS is the victim?
Not so fast, again.
You see, in real situations, we don't necessarily know who we play. We're just a bunch of strategies playing games. I may figure out "what kind of animal" you are after a couple of moves. But within a population of coexisting agents, you know, the kind that evolves according to the rules that Charles Darwin discovered, you play with those you meet.
And in that case, you, the domineering ZD strategist, may just as well run into another ZD strategist! For all you know, that ZD player may be one of your offspring!
What does ZD get against another ZD? I'll let you think this over for a few seconds.
Tic
Toc
Tic
Toc
Keep in mind, ZD forces ANY strategy to accept a fixed payoff.
Tic
Toc
ZD must accept the same payoff she forces on others when playing against other ZDs!
But that is terrible! Because once ZD has gained a foothold in a population that ZD can rip off, that means that ZD has achieved a sizable population fraction. Which means that ZD is going to have to play against versions of itself more and more. And fare terribly, just like all the other schmuck strategies she rips off.
But, what if the schmuck strategy plays really well against itself? Like, cooperates and reaps a mean payoff of 3?
You know, like, for example, WSLS?
That would mean that ZD would be doomed even though it wins every single friggin' battle with WSLS! Every one! But at some point, it becomes clear that winning isn't everything. You've got to be able to play with your own kind. WSLS does that well. ZD... not so much. ZD will take your lunch money, and ends up eating its own lunch too. How perfectly, weirdly, appropriate.
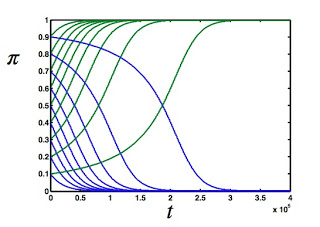
I'll leave you with the plot that proves this point, which is almost the one that appeared on the MIT Technology Review post that stated that the world of Game Theory is on fire. In that plot, the green lines show the fraction of the population that is WSLS, while the blue lines show the ZD fraction for different starting fractions. For example, if ZD (blue line) starts at 0.9, it competes with a green line that starts at 0.1. And green wins, no matter how many ZDs there are at the outset. The bully gets her come-uppance!
The plot looks the same as what appeared on MIT Technology Review, but on the original blog post they used a figure from the first version of the paper, where we showed that ZD would lose against All-D in a population setting. We realized soon after that using All-D is not such a great example, because All-D wins against ZD in direct competition too. So we chose WSLS to make our point instead. But it doesn't really matter. ZD sucks because it is so mean, and has no choice to also be mean against "its own kind". That's what takes it down.
If I was naive, I'd draw parallels to politics right here at the conclusion. But I'm not that naive. These are games that we investigated. Games that agents play. There, winning isn't everything, because karma is a bitch, so to speak. In real life, we are still searching for definitive answers.
These results (and a whole lot more) are described in more detail in the publication, available via open access:
C. Adami and A. Hintze: Evolutionary instability of zero-determinant strategies demonstrates that winning is not everything: Nature Communications 4 (2013) 2193.