Black holes and the fate of quantum information

I have written about the fate of classical information interacting with black holes fairly extensively on this blog (see Part 1, Part 2, and Part 3). Reviewers of the article describing those results nearly always respond that I should be considering the fate of quantum, not classical information. 

In particular, they ask me to comment on what all this means in the light of more modern controversies, such as black hole complementarity and firewalls. As if solving the riddle of what happens to classical information is not nearly good enough. 

I should first state that I disagree with the idea that it is necessary to discuss the fate of quantum information in an article that discusses what happens to classical information. I'll point out the differences between those two concepts here, and hopefully I'll convince you that it is perfectly reasonable to discuss these independently. However, I have given in to these requests, and now written an article (together with my colleague Kamil Bradler at St. Mary's University in Halifax, Canada) that studies the fate of quantum information that interacts with a black hole. Work on this manuscript explains (in part) my prolonged absence from blogging.

The results we obtained, it turns out, do indeed shed new light on these more modern controversies, so I'm grateful for the reviewer's requests after all. The firewalls have "set the physics world ablaze", as one blogger writes. These firewalls (that are suggested to surround a black hole) have been invented to correct a perceived flaw in another widely discussed theory, namely the theory of black hole complementarity due to the theoretical physicist Leonard Susskind. I will briefly describe these in more detail below, but before I can do this, I have to define for you the concept of quantum entanglement.

Quantum entanglement lies at the very heart of quantum mechanics, and it is what makes quantum physics different from classical physics. It is clear, as a consequence, that I won't be able to make you understand quantum entanglement if you have never studied quantum mechanics. If this is truly your first exposure, you should probably consult the Wiki page about quantum entanglement, which is quite good in my view. 

Quantum entanglement is an interaction between two quantum states that leaves them in a joint state that cannot be described in terms of the properties of the original states. So, for example, two quantum states $\psi_A$ and $\psi_B$ may have separate properties before entanglement, but after they interact they will be governed by a single wavefunction $\psi_{AB}$ (there are exceptions). So for example, if I imagine a wavefunction $\psi_A=\sigma|0\rangle +\tau|1\rangle$ (assuming the state to be correctly normalized) and a quantum state B simply given by $|0\rangle$, then a typical entangling operation $U$ will leave the joint state entangled:

      $U(\sigma|0\rangle +\tau|1\rangle)|0\rangle=\sigma|00\rangle +\tau|11\rangle$.    (1)

The wavefunction on the right hand side is not a product of the two initial wavefunctions, and in any case classical systems can never be brought into such a superposition of states in the first place. Another interesting aspect of quantum entanglement is that it is non-local. If A and B represent particles, you can still move one of the particles far away (say, to another part in the galaxy). They will still remain entangled. Classical interactions are not like that. At all.

A well-known entangled wavefunction is that of the Einstein-Podolsky-Rosen pair, or EPR pair. This is a wavefunction just like (1), but with $\sigma=\tau=1/\sqrt{2}$. The '0' vs '1' state can be realized via any physical quantum two-state system, such as a spin 1/2-particle or a photon carrying a horizontal or vertical polarization. 

What does it mean to send quantum information? Well, it just means sending quantum entanglement! Let us imagine a sender Alice, who controls a two-state quantum system that is entangled with another system (let us call it $R$ for "reference"), this means that her quantum wavefunction (with respect to $R$) can be written as 

                $|\Psi\rangle_{AR}=\sigma|00\rangle_{AR} +\tau|11\rangle_{AR}$    (2)

where the subscripts $AR$ refer to the fact that the wavefunction now "lives" in the joint space $AR$. $A$ and $R$ (after entanglement) do not have individual states any longer.

Now, Alice herself should be unaware of the nature of the entanglement between $A$ and $R$ (meaning, Alice does not know the values of the complex constants $\sigma$ and $\tau$). She is not allowed to know them, because if she did, then the quantum information she would send would become classical. Indeed, Alice can turn any quantum information into classical information by measuring the quantum state before sending it. So let's assume Alice does not do this. She can still try to send the arbitrary quantum state that she controls to Bob, so that after the transmittal her quantum state is unentangled with $R$, but it is now Bob's wavefunction that reads

           $|\Psi\rangle_{BR}=\sigma|00\rangle_{BR} +\tau|11\rangle_{BR}$    (3). 

In this manner, entanglement was transferred from $A$ to $B$. That is a quantum communication channel.

Of course, lots of things could happen to the quantum entanglement on its way to Bob. For example, it could be waylayed by a black hole. If Alice sends her quantum entanglement into a black hole, can Bob retrieve it? Can Bob perform some sort of magic that will leave the black hole unentangled with $A$ (or $R$), while he himself is entangled as in (3)?

Whether or not Bob can do this depends on whether the quantum channel capacity of the black hole is finite, or whether it vanishes. If the capacity is zero, then Bob is out of luck. The best he can do is to attempt to reconstruct Alice's quantum state using classical state estimation techniques. That's not nothing by the way, but the "fidelity" of the state reconstruction is at most 2/3. But I'm getting ahead of myself.

Let's first take a look at this channel. I'll picture this in a schematic manner where the outside of the black hole is at the bottom, and the inside of the black hole is at the top, separated by the event horizon. Imagine Alice sending her quantum state in from below. Now, black holes (as all realistic black bodies) don't just absorb stuff: they reflect stuff too. How much is reflected depends on the momentum and angular momentum of the particle, but in general we can say that a black hole has an absorption coefficient $0\leq\alpha\leq1$, so that $\alpha^2$ is just the probability that a particle that is incident on the black hole is absorbed.

So we see that if $n$ particles are incident on a black hole (in the form of entangled quantum states $|\psi\rangle_{\rm in}$), then $(1-\alpha^2)n$ come out because they are reflected at the horizon. Except as we'll see, they are in general not the pure quantum states Alice sent in anymore, but rather a mixture $\rho_{\rm out}$. This is (as I'll show you) because the black hole isn't just a partially silvered mirror. Other things happen, like Hawking radiation. Hawking radiation is the result of quantum vacuum fluctuations at the horizon, which constantly create particle-antiparticle pairs. If this happened anywhere but at the event horizon, the pairs would annihilate back, and nobody would be the wiser. Indeed, such vacuum fluctuations happen constantly everywhere in space. But if it happens at the horizon, then one of the particles could cross the horizon, while the other (that has equal and opposite momentum), speeds away from it. That now looks like the black hole radiates. And it happens at a fixed rate that is determined by the mass of the black hole. Let's just call this rate $\beta^2$.

As you can see, the rate of spontaneous emission does not depend on how many particles Alice has sent in. In fact, you get this radiation whether or not you throw in a quantum state. These fluctuations go on before you send in particles, and after. They have absolutely nothing to do with $|\psi\rangle_{\rm in}$. They are just noise. But they are (in part) responsible for the fact that the reflected quantum state $\rho_{\rm out}$ is not pure anymore. 

But I can tell you that if this were the whole story, then physics would be in deep deep trouble. This is because you cannot recover even classical information from this channel if $\alpha=1$. Never mind quantum. In fact, you could not recover quantum information even in the limit $\alpha=0$, a perfectly reflecting black hole! (I have not shown you this yet, but I will). 

This is not the whole story, because a certain gentleman in 1917 wrote a paper about what happens when radiation is incident on a quantum mechanical black body. Here is a picture of this gentleman, along with the first paragraph of the 1917 paper:

Albert Einstein in 1921  (source: Wikimedia) 

 In Einstein's 1917 article "On the quantum theory of radiation" what Einstein discovered in that paper is that you can derive Planck's Law (about the distribution of radiation emanating from a black body) using just the quantum mechanics of absorption, spontaneous emission, and stimulated emission of radiation. Stimulated emission is by now familiar to everybody, because it is the principle upon which Lasers are built. What Einstein showed in that paper is that stimulated emission is an inevitable consequence of absorption: if a black body absorbs radiation, it also stimulates the emission of radiation, with the same exact quantum numbers as the incoming radiation.

Here's the figure from the Wiki page that shows how stimulated emission makes "two out of one":

Quantum "copying" during stimulated emission from an atom (source: Wikimedia)

In other words, all black bodies are quantum copying machines!

"But isn't quantum copying against the law?"

Actually, now that you mention it, yes it is, and the law is much more stringent than the law against classical copying (of copy-righted information, that is). The law (called the no-cloning theorem) is such that it cannot--ever--be broken, by anyone or anything. 

The reason why black bodies can be quantum copying machines is that they don't make perfect copies, and the reason the copies aren't perfect is the presence of spontaneous emission, which muddies up the copies. This has been known for 30 years mind you, and was first pointed out by the German-American physicist Leonard Mandel. Indeed, only perfect copying is disallowed. There is a whole literature on what is now known as "quantum cloning machines" and it is possible to calculate what the highest allowed fidelity of cloning is. When making two copies from one, the highest possible fidelity is $F$=5/6. That's an optimal 1->2 quantum cloner. And it turns out that in a particular limit (as I point out in this paper from 2006) black holes can actually achieve that limit!  I'll point out what kind of black holes are optimal cloners further below.

All right, so now we have seen that black holes must stimulate the emission of particles in response to incoming radiation. Because Einstein said they must. The channel thus looks like this:

In addition to the absorbed/reflected radiation, there is spontaneous emission (in red), and there is stimulated emission (in blue). There is something interesting about the stimulated "clones". (I will refer to the quantum copies as clones even though they are not perfect clones, of course. How good they are is central to what follows). 

Note that the clone behind the horizon has a bar over it, which denotes "anti". Indeed, the stimulated stuff beyond the horizon consists of anti-particles, and they are referred to in the literature as anti-clones, because the relationship between $\rho_{\rm out}$ and $\bar \rho_{\rm out}$ is a quantum mechanical NOT operation. (Or, to be technically accurate, the best NOT you can do without breaking quantum mechanics.) That the stimulated stuff inside and outside the horizon must be particles and anti-particles is clear, because the process must conserve particle number. We should keep in mind that the Hawking radiation also conserves particle number. The total number of particles going in is $n$, which is also the total number of particles going out (adding up stuff inside and outside the horizon). I checked. 

Now that we know that there are a bunch of clones and anti-clones hanging around, how do we use them to transfer the quantum entanglement? Actually, we are not interested here in a particular protocol, we are much more interested in whether this can be done at all. If we would like to know whether a quantum state can be reconstructed (by Bob) perfectly, then we must calculate the quantum capacity of the channel. While how to do this (and whether this calculation can be done at all) is technical, one thing is not: If the quantum capacity is non-zero then, yes, Bob can reconstruct Alice's state perfectly (that is, he will be entangled with $R$ exactly like Alice was when he's done). If it is zero, then there is no way to do this, period.

In the paper I'm blogging about, Kamil and I did in fact calculate the capacity of the black hole channel, but only for two special cases: $\alpha=0$ (a perfectly reflecting black hole), and $\alpha=1$ (a black hole that reflects nothing). The reason we did not tackle the general case is that at the time of this writing, you can only calculate the quantum capacity of the black hole channel exactly for these two limiting cases. For a general $\alpha$, the best you can do is give a lower and an upper bound, and we have that calculation planned for the future. But the two limiting cases are actually quite interesting.

[Note: Kamil informed me that for channels that are sufficiently "depolarizing", the capacity can in fact be calculated, and then it is zero. I will comment on this below.]

First: $\alpha=0$. In that case the black hole isn't really a black hole at all, because it swallows nothing. Check the figure up there, and you'll see that in the absorption/reflection column, you have nothing in black behind the horizon. Everything will be in front. How much is reflected and how much is absorbed doesn't affect anything in the other two columns, though. So this black hole really looks more like a "white hole", which in itself is still a very interesting quantum object. Objects like that have been discussed in the literature (but it is generally believed that they cannot actually form from gravitational collapse). But this is immaterial for our purposes: we are just investigating here the quantum capacity of such an object in some extreme cases. For the white hole, you now have two clones outside, and a single anticlone inside (if you would send in one particle). 

Technical comment for experts: 

A quick caveat: Even though I write that there are two clones and a single anti-clone after I send in one particle, this does not mean that this is the actual number of particles that I will measure if I stick out my particle detector, dangling out there off of the horizon. This number is the mean expected number of particles. Because of vacuum fluctuations, there is a non-zero probability of measuring a hundred million particles. Or any other number.  The quantum channel is really a superposition of infinitely many cloning machines, with the 1-> 2 cloner the most important. This fundamental and far-reaching result is due to Kamil. 

So what is the capacity of the channel? It's actually relatively easy to calculate because the channel is already well-known: it is the so-called Unruh channel that also appears in a quantum communication problem where the receiver is accelerated, constantly. The capacity looks like this:

Quantum capacity of the white hole channel as a function of z

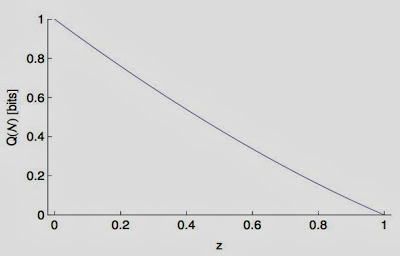
In that figure, I show you the capacity as a function of $z=e^{-\omega/T}$, where $T$ is the temperature of the black hole and $\omega$ is the frequency (or energy) of that mode. For a very large black hole the temperature is very low and, as a consequence, the channel isn't very noisy at all (low $z$). The capacity therefore is nearly perfect (close to 1 bit decoded for every bit sent). When black holes evaporate, they become hotter, and the channel becomes noisier (higher $z$). For infinitely small black holes ($z=1$) the capacity finally vanishes. But so does our understanding of physics, of course, so this is no big deal. 

What this plot implies is that you can perfectly reconstruct the quantum state that Alice daringly sent into the white hole as long as the capacity $Q$ is larger than zero. (If the capacity is small, it would just take you longer to do the perfect reconstructing.). I want to make one thing clear here: the white hole is indeed an optimal cloning machine (the fidelity of cloning 1->2 is actually 5/6, for each of the two clones). But to recreate the quantum state perfectly, you have to do some more work, and that work requires both clones. But after you finished, the reconstructed state has fidelity $F=1$.) 

"Big deal" you might say, "after all the white hole is a reflector!"

Actually, it is a somewhat big deal, because I can tell you that if it wasn't for that blue stimulated bit of radiation in that figure above, you couldn't do the reconstruction at all! 

"But hold on hold on", I hear someone mutter, from far away. "There is an anti-clone behind the horizon! What do you make of that? Can you, like, reconstruct another perfect copy behind the horizon? And then have TWO?"

So, now we come to the second result of the paper. You actually cannot. The capacity of the channel into the black hole (what is known as the complementary channel) is actually zero because (and this is technical speak) the channel into the black hole is entanglement breaking. You can't reconstruct perfectly from a single clone or anti-clone, it turns out. So, the no-cloning theorem is saved. 

Now let's come to the arguably more interesting bit: a perfectly absorbing black hole ($\alpha$=1). By inspecting the figure, you see that now I have a clone and an anti-clone behind the horizon, and a single clone outside (if I send in one particle). Nothing changes in the blue and red lines. But everything changes for the quantum channel. Now I can perfectly reconstruct the quantum state behind the horizon (as calculating the quantum capacity will reveal), but the capacity in front vanishes! Zero bits, nada, zilch. If $\alpha=1$, the channel from Alice to Bob is entanglement breaking.  

It is as if somebody had switched the two sides of the black hole! 

Inside becomes outside, and outside becomes inside!

Now let's calm down and ponder what this means. First: Bob is out of luck. Try as he might, he cannot have what Alice had: the same entanglement with $R$ that she enjoyed. Quantum entanglement is lost when the black hole is perfectly absorbing. We have to face this truth.  I'll try to convince you later that this isn't really terrible. In fact it is all for the good. But right now you may not feel so good about it.

But there is some really good news. To really appreciate this good news, I have to introduce you to a celebrated law of gravity, the equivalence principle. 

The principle, due to the fellow whose pic I have a little higher up in this post, is actually fairly profound. The general idea is that an observer should not be able to figure out whether she is, say, on Earth being glued to the surface by 1g, or whether she is really in a spaceship that accelerates at the rate of 1g (g being the constant of gravitational acceleration on Earth, you know: 9.81 m/sec$^2$). The equivalence principle has far reaching consequences. It also implies that an observer (called, say, Alice), who falls towards (and ultimately into) a black hole, should not be able to figure out when and where she passed the point of no return. 

The horizon, in other words, should not appear as a special place to Alice at all. But if something dramatic would happen to quantum states that cross this boundary, Alice would have a sure-fire way to notice this change: she could just keep the quantum state in a protected manner at her disposition, and constantly probe this state to find out if anything happened to it. That's actually possible using so-called "non-demolition" experiments. So, unless you feel like violating another one of Einstein's edicts (and, frankly, the odds are against you if you do), you better hope nothing happens to a quantum state that crosses from the outside to the inside of a black hole in the perfect absorption case ($\alpha=1$). 

Fortunately, we proved (result No. 3) that you can perfectly reconstruct the state behind the horizon when $\alpha=1$, that this capacity is non-zero. And that as a consequence, the equivalence principle is upheld. 

This may not appear to you as much of a big deal when you read this, but many many researchers have been worried sick about this, that the dynamics they expect in black holes would spell curtains for the equivalence principle. I'll get back to this point, I promise. But before I do so, I should address a more pressing question.

"If Alice's quantum information can be perfectly reconstructed behind the horizon, what happens to it in the long run?"

This is a very serious question. Surely we would like Bob to be able to "read" Alice's quantum message (meaning he yearns to be entangled just like she was). But this message is now hidden behind the black hole event horizon. Bob is a patient man, but he'd like to know: "Will I ever receive this quantum info?"

The truth is, today we don't know how to answer this question. We understand that Alice's quantum state is safe and sound behind the horizon--for now. There is also no reason to think that the on going process of Hawking radiation (that leads to the evaporation of the black hole) should affect the absorbed quantum state. But at some point or other, the quantum black hole will become microscopic, so that our cherished laws of physics may lose their validity. At that point, all bets are off. We simply do not understand today what happens to quantum information hidden behind the horizon of a black hole, because we do not know how to calculate all the way to very small black holes. 

Having said this, it is not inconceivable that at the end of a black hole's long long life, the only thing that happens is the disappearance of the horizon. If this happens, two clones are immediately available to an observer (the one that used to be on the outside, and the one that used to be inside), and Alice's quantum state could finally be resurrected by Bob, a person that no doubt would merit to be called the most patient quantum physicist in the history of all time. 

Now what does this all mean for black hole physics?

I have previously shown that classical information is just fine, and that the universe remains predictable for all times. This is because to reconstruct classical information, a single stimulated clone is enough. It does not matter what $\alpha$ is, it could even be one. Quantum information can be conveyed accurately if the black hole is actually a white hole, but if it is utterly black then quantum information is stuck behind the horizon, even though we have a piece of it (a single clone) outside of the horizon. But that's not enough, and that's a good thing too, because we need the quantum state to be fully reconstructable inside of the black hole, otherwise the equivalence principle is hosed.  And if it reconstructable inside, then you better hope it is not reconstructable outside, because otherwise the no-cloning theorem would be toast. 

So everything turns out to be peachy, as long as nothing drastic happens to the quantum state inside the black hole. We have no evidence of something so drastic, but at this point we simply do not know. 

Now what are the implications for black hole complementarity? The black hole complementarity principle was created from the notion (perhaps a little bit vague) that, somehow, quantum information is both reflected and absorbed by the black hole channel at the same time. Now, given that you have read this far in this seemingly interminable post, you know that this is not allowed. It really isn't. What Susskind, Thorlacius, and 't Hooft argued for, however, is that it is OK as long as you won't be caught. Because, they argued, nobody will be able to measure the quantum state on both sides of the horizon at the same time anyway!

Now I don't know about you, but I was raised believing that just because you can't be caught it doesn't make it alright to break the rules.  And what our more careful analysis of quantum information interacting with a black hole has shown, is that you do not break the quantum cloning laws at all. Both the equivalence principle and the no-cloning theorem are perfectly fine. Nature just likes these laws, and black holes are no outlaws.

Adventurous Alice encounters a firewall? Credit: Nature.com

What about firewalls then? Quantum firewalls were proposed to address a perceived inconsistency in the black hole complementarity picture. But you now already know that that picture was inconsistent to begin with. Violating no-cloning laws brings with it all kinds of paradoxes. Unfortunately, the firewall hypothesis just heaped paradoxes upon paradoxes, because it proposed that you have to violate the equivalence principle as well. This is because that hypothesis assumes that all the information was really stored in the Hawking radiation (the red stuff in the figures above). But there is really nothing in there, so that the entire question of whether transmitting quantum information from Alice to Bob violates the concept of "monogamy of entanglement" is moot. The Hawking radiation can be entangled with the black hole, but it is no skin off of Alice or Bob, that entanglement is totally separate. 

So, all is well, it seems, with black holes, information, and the universe. We don't need firewalls, and we do not have to invoke a "complementarity principle". Black hole complementarity is automatic, because even though you do not have transmission when you have perfect reflection, a stimulated clone does make it past the horizon. And when you have perfect transmission ($\alpha$=1) a stimulated clone still comes back at you. So it is stimulated emission that makes black hole complementarity possible, without breaking any rules. 

Of course we would like to know the quantum capacity for an arbitrary $\alpha$, which we are working on. One result is already clear: if the transmission coefficient $\alpha$ is high enough that not enough of the second clone is left outside of the horizon, then the capacity abruptly vanishes. Because the black hole channel is a particular case of a "quantum depolarizing channel", discovering what this critical $\alpha$ is only requires mapping the channel's error rate $p$ to $\alpha$. 

I leave you with an interesting observation. Imagine a black hole channel with perfect absorption, and put yourself into the black hole. Then, call yourself "Complementary Alice", and try to send a quantum state across the horizon. You immediately realize that you can't: the quantum state will be reflected. The capacity to transmit quantum information out of the black hole vanishes, while you can perfectly communicate quantum entanglement with "Complementary Bob". Thus, from the inside of the perfectly absorbing black hole it looks just like the white hole channel (and of course the reverse is true for the perfectly reflecting case). Thus, the two channels are really the same, just viewed from different sides! 

This becomes even more amusing if you keep in mind that (eternal) black holes have white holes in their past, and white holes have black holes in their future. 

The curious case of the lethal publication

Disclaimer: I refuse to believe anything I wrote below. And so should you :-)

I have a confession to make. I think I may have been responsible for the demise of some very eminent scientists. Unwittingly, and unwillingly, of course. But the evidence is really quite damning, and I shudder to think what horrible deed I will commit next. Perhaps the only way for me to clear my conscience is by coming clean with the whole story. So bear with me here, as I free myself from this heavy burden.

It all began in 1986, when I started graduate school in Physics at Stony Brook University on Long Island. I had worked on solitons in nonlinear field theories already at Bonn University, but had never published anything about them. These solitons, called "Skyrmions" after their inventor Tony Skyrme, were supposed to be a good model of the nucleon. I wrote two papers about them in 1987. Shortly after publication of the first, Tony Skyrme died mysteriously (he was only 64). It said, at the time, that he died from an error in anesthesia while undergoing routine knee surgery, and I certainly believed it. Today I am not so sure anymore. I think I am to blame. When I write papers about somebody's life work, it seems like I seal their fate.

But I'm getting ahead of myself. Surely this was just a coincidence. It was just a pair of papers--and the second one was only published in 1988, because the publisher had lost the manuscript at one point. Yes, we sent in manuscripts by mail during the olden days. 

When I turned my attention from nuclear physics to theoretical biology, one of my first papers was on the concept of self-organized criticality, invented and championed by the physicist Per Bak. Per and I were  friends for the most part. He would tell me about how he handled submissions to the journal Physical Review Letters when he was editor there, and how that got him fired. (When the stack of manuscripts on the desk of a fellow editor got too tall, he just sent "accepted" notices out to all of the authors. Those were the days.) But the publication of my article "Self-organized criticality in living systems" was not something he seemed to be very fond of. I know that because I have good evidence that he was the referee on the submission to Science magazine that was ultimately unsuccessful. Anyway, he did not survive that publication. He passed away in circumstances that are quite shocking. I'm still sadddened by it. And, looking back, I feel even more guilty. 

But, I'm sure you understand, I had no inkling at that point that I wielded some sort of nefarious power. I was just following my career, publishing papers in the areas that interested me. And at that point in time, I had become interested in the theory of computation, mainly because I started to work in the field  of quantum computation. One of the seminal people in this area was Rolf Landauer, who showed that the only thing that costs you energy in a computational process is the act of erasure. I even sat next to him at a dinner once! But why did I just have to write this paper on "Complexity, Computation, and Measurement" in 1996, where I introduced the concept of "Landauer machines"? Rolf was a hero of mine, but unfortunately that paper was just too much. It was not long after it was published that Rolf succumbed. 

Naturally I could still ascribe all this to circumstance, and certainly I did. So when I wrote a paper about "Entropic Bell Inequalities" in 1996, I was not worried. After all, John Bell had died in 1990, and the other people possibly inolved in this work were those that created the concept of "EPR pairs" that were so fundamental to that paper. "EPR" stands for "Einstein-Podolsky-Rosen", of course. Einstein died in 1955, Boris Podolsky in 1966, and Nathan Rosen in.. Oh no! Rosen was still alive when we wrote our paper! But he was 86 already, and so it was just natural that he passed on even while our paper was still in revision. Or was it?

After this experience, I learned to be more careful. For example, I learned that if you write a paper together with the person whose seminal contribution you address, that person is safe. This is how Ismail Zahed and Gerry Brown survived the onslaught of my publications. And I felt safe writing papers on the classical theory of information, because its originator (the eminent Claude Shannon) was surely dead by the time I ventured on the scene. My article on the "Physical Complexity of Symbolic Sequences" that appeared in 2000 showed that you could use Shannon information as a proxy for the complexity of biomolecular sequences in general. But, I had no idea that Shannon was still alive. Nobody knew! He would go around to information theory conferences, listening to conversations between researchers during breaks, and then introduce himself. Of course, nobody would believe he was Shannon! 

So Shannon was alive after all, until this cursed paper of mine appeared! Another hero of mine slain! I was dumbfounded. Mortified. I vowed never to write a paper again. 

But you know that I could not keep this up for long. Like you yourself would have done, I shrugged this off as pure coincidence mixed with a pinch of paranoia. After all, Landauer and Shannon were old. It wasn't me, I repeated to myself. So I started on another project: to understand the abundance distribution of species. These distributions are fairly general: you can write down distributions of any taxon, as a function of how many subtaxa each taxon generated. So, for example, I wanted to know what is the distribution of number of species that each genus has created, or the distribution of genus sizes (number of genera) that each family generated, and so on. With my student Johan Chu, I developed a theory that would predict these disctributions based on only two (and sometimes just one) parameter, using the theory of branching processes. To test the theory, we wrote to John Sepkoski, a paleontologist at the University of Chicago, who as his life's work has created data sets (compendia) of marine animal families and genera. He kindly sent us his compendia, which we used for our paper that ultimately appeared in the Proceedings of the National Academy. John was 50 at the time, so surely he was safe.

But he was not. John Sepkoski passed away at the age of 50 of an apparent heart attack, just before my paper appeared in print. My heart broke a little too. What is this curse?

Could it get any worse? What if I wrote a paper on the growth of complexity in biology, a subject that is very near to the heart of eminent evolutionary biologist and paleontologist Stephen J. Gould? Could my paper "What is Complexity?" that appeared in 2002 have anything to do with his sudden passing? Perhaps I should not have addressed the concept of "punctuated equilibrium", one of hist best-known contributions?
 

I can't go on. I don't want to look at the list of my publications anymore, for fear of what I might find. Best not to think about it anymore. I hope that my upcoming paper in Nature Communications about a certain type of strategy in game theory (so-called ZD strategies) doesn't have any negative consequences for anyone. Bill Press, one of the co-authors of the original paper on ZD strategies is 65 and in perfect health, as far as I know. And Press's co-author, the eminent Freeman Dyson is... oh oh. Dyson is 89.